11.1.2 极小值优化 1．标量最小值优化 求解单变量最优化问题的方法有多种，根据目标函数是否需要求导，可以分为两类，即直接法和间接法。直接法不需要对目标函数进行求导，而间接法则需要用到目标函数的导数。 常用的一维直接法主要有消去法和近似法两种。 （1）消去法：该法利用单峰函数具有的消去性质进行反复迭代，逐渐消去不包含极小点的区间，缩小搜索区间，直到搜索区间缩小到给定的允许精度为止。一种典型的消去法为黄金分割法（Golden Section Search）。黄金分割法的基本思想是在单峰区间内适当地插入两点，将区间分为3段，然后通过比较这两点函数值的大小来确定是删去最左段还是最右段，或同时删去左右两段，而保留中间段。重复该过程可以使区间无限缩小。插入点的位置放在区间的黄金分割点及其对称点上，所以该法称为黄金分割法。该法的优点是算法简单，效率较高，稳定性好。 （2）多项式近似法：该法用于目标函数比较复杂的情况。此时搜索一个与它近似的函数代替目标函数，并用近似函数的极小点作为原函数极小点的近似。常用的近似函数为二次和三次多项式。二次插值法的计算速度比黄金分割法快，但是对于一些强烈扭曲或可能多峰的函数，该法的收敛速度会变得很慢，甚至失败。 间接法需要计算目标函数的导数，优点是计算速度很快。常见的间接法包括牛顿切线法、对分法、割线法和三次插值多项式近似法等。优化工具箱中用得较多的是三次插值法。如果函数的导数容易求得，一般来说应首先考虑使用三次插值法，因为它具有较高的效率。在只需要计算函数值的方法中，二次插值法是一个很好的方法，它的收敛速度较快，特别是在极小点所在区间较小时尤为如此。黄金分割法则是一种十分稳定的方法，并且计算简单。基于以上分析，MATLAB优化工具箱中使用得较多的方法是二次插值法、三次插值法、二次三次混合插值法和黄金分割法。 MATLAB优化工具箱提供了fminbnd函数来进行标量最小值问题的优化求解，其调用语法如下。 （1）x = fminbnd(fun,x1,x2)：返回标量函数fun在条件x1 < x < x2下取最小值时自变量x的值。 （2）x = fminbnd(fun,x1,x2,options)：用options参数指定的优化参数进行最小化。 （3）x = fminbnd(problem)：求解problem的最小值，其中problem是一个用输入变量来表达的结构数组。 （4）[x,fval] = fminbnd(...)：返回解x处目标函数的值fval。 （5）[x,fval,exitflag] = fminbnd(...)：返回exitflag值描述fminbnd函数的退出条件。 （6）[x,fval,exitflag,output] = fminbnd(...)：返回包含优化信息的结构数组output。 其中fun为需要最小化的目标函数。fun函数需要输入标量参数x，返回x处的目标函数标量值f。fun可以是一个匿名函数的函数句柄，如下所示： x = fminbnd(inline('sin(x*x)'),x0) 同样，fun参数也可以是一个包含函数名的字符串，对应的函数可以是M文件、内部函数或MEX文件。options为优化参数选项，用户可以用optimset函数设置或改变参数的值。至于options参数的具体设置，读者可自行查阅帮助文档。 【例11-1】 对边长为3m的正方形铁板，在4个角处剪去相等的正方形，以制成方形无盖水槽，问如何剪才能使水槽的容积最大？ 假设剪去的正方形的边长为x，则水槽的容积为： 现在要求在区间（0,1.5）上确定一个x，使V最大化。因为优化工具箱中要求目标函数最小化，所以需要对目标函数进行转换：V1=-V，即要求V1的最小值。 首先编写此问题的函数M文件： myfun1.m function f = myfun1(x) f = -(3-2*x).^2 * x; 然后在命令行调用fminbnd函数： >> x = fminbnd(@myfun1,0,1.5) x = 0.5000 即剪掉的小正方形的边长为0.5m时水槽的容积最大。我们可以调用myfun1函数来计算水槽的最大容积： >> y= -myfun1(x) y = 2.0000 水槽的最大容积为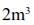 。 2．无约束最小值优化 无约束最优化问题在实际应用中也比较常见，如工程中常见的参数反演问题。另外，许多有约束最优化问题也可以转化为无约束最优化问题进行求解。 求解无约束最优化问题的方法主要有两类，即直接搜索法（Search method）和梯度法（Gradient method）。 直接搜索法适用于目标函数高度非线性，没有导数或导数很难计算的情况。实际工程中很多问题都是非线性的，因此直接搜索法不失为一种有效的解决办法。常用的直接搜索法为单纯形法，此外还有Hooke-Jeeves搜索法、Pavell共轭方向法等，其缺点是收敛速度慢。 在函数的导数可求的情况下，梯度法是一种更优的方法，该法利用函数的梯度（一阶导数）和Hessian矩阵（二阶导数）构造算法，可以获得更快的收敛速度。函数f(x)的负梯度方向即反映了函数的最大下降方向。当搜索方向取为负梯度方向时，称为最速下降法。但当需要最小化的函数有一狭长的谷形值域时，该法的效率则很低。常见的梯度法有最速下降法、Newton法、Marquart法、共轭梯度法和拟牛顿法（Quasi-Newton method）等。在这些方法中，用得最多的是拟牛顿法。 在MATLAB中，有fminunc和fminsearch两个函数用来求解无约束最优化问题。由于MATLAB优化工具箱表11-1中列出的函数调用语法和参数说明都比较类似，同时篇幅有限，所以下面只举例来说明一下这些函数的用法。 【例11-2】 求函数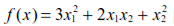 的最小值。 首先编写函数的M文件。需要注意的是：本例中的目标函数具有两个变量，在编写函数的时候需要将这两个自变量作为列向量输入目标函数。M文件的具体内容如下： myfun2.m function f = myfun2(x) f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2; % 目标函数 然后在命令行调用fminunc函数来寻找目标函数在点［1,1］附近的最小值： x0 = [1,1]; [x,fval] = fminunc(@myfun2,x0) fminunc函数经过多次迭代之后，给出如下计算结果： x = % 最小值所对应的x值 1.0e-006 * 0.2541 -0.2029 fval = % 最小值的大小 1.3173e-013 【例11-3】 求banana方程的最小值： 通过分析可知，最小值0所对应的点为(a,a2)。可以在指定a的情况下求这个方程的最小值，例如让a = sqrt(2)。下面来创建一个包含参数a的匿名函数： >> a = sqrt(2); >> banana = @(x)100*(x(2)-x(1)^2)^2+(a-x(1))^2; 然后在MATLAB命令行中输入以下命令： >> [x,fval,exitflag] = fminsearch(banana, [-1.2, 1], ... optimset('TolX',1e-8)) % optimset('TolX',1e-8)用来设置算法终止误差 x = 1.4142 2.0000 fval = 4.2065e-018 exitflag = 1 在点(sqrt(2), 2)得到了函数的最小值，fval非常接近于0，这说明本例中fminsearch函数的优化计算是非常成功的。 3．线性规划 线性规划是处理线性目标函数和线性约束的一种较为成熟的方法，目前已经广泛地应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。线性规划问题的标准形式是： 写成矩阵形式为： 其中： 线性规划的标准形式要求目标函数最小化，约束条件取等式，变量非负。不符合这几个条件的线性模型要首先转换成标准形。线性规划的求解方法主要是单纯形法。 MATLAB优化工具箱提供了linprog函数用来进行线性规划的求解。 【例11-4】 求如下函数的最小值。 首先在MATLAB命令行中输入以下参数： >> f = [-5; -4; -6]; % 用矩阵表示目标函数 >> A = [1 -1 1 3 2 4 3 2 0]; % 用矩阵形式表示约束条件系数 >> b = [20; 42; 30]; % 约束条件 >> lb = zeros(3,1); % 下界约束 然后调用linprog函数： >> [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb); Optimization terminated. >> x,lambda.ineqlin,lambda.lower % 显示结果 x = 0.0000 15.0000 3.0000 ans = 0.0000 1.5000 % 主动约束 0.5000 % 主动约束 ans = 1.0000 % 主动约束 0.0000 0.0000 Lambda域中向量里的非零元素可以反映出求解过程中的主动约束。在本例的结果中可以看出，第2个和第3个不等式约束（lambda.ineqlin）和第1个下界约束（lambda.lower）是主动约束。 4．二次规划 二次规划是非线性规划中一类特殊的数学规划问题，它的解是可以通过求解得到的。通常通过解其库恩-塔克条件（K-T条件），获取一个K-T条件的解，称为K-T对，其中与原问题的变量对应的部分称为K-T点。二次规划的一般形式为： 其中为对称矩阵。二次规划分为凸二次规划与非凸二次规划两者，前者的K-T点便是其全局极小值点，而后者的K-T点则可能连局部极小值点都不是。若它的目标函数是二次函数，则约束条件是线性的。求解二次规划的方法很多，较简便易行的是沃尔夫法，它是依据K-T条件，在线性规划单纯形法的基础上加以修正而得到的。此外还有莱姆基法、毕尔法、凯勒法等。 MATLAB优化工具箱中提供了quadprog函数用来进行二次规划的求解。 【例11-5】 求下面函数的最小值。 首先，我们注意到这个方程可以用矩阵形式来表示： 其中： 在MATLAB命令行中输入以下参数命令： >> H = [1 -1; -1 2]; >> f = [-2; -6]; >> A = [1 1; -1 2; 2 1]; % 线性不等式约束 >> b = [2; 2; 3]; % 线性不等式约束 >> lb = zeros(2,1); 然后调用二次规划函数quadprog： >> [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb) Optimization terminated. x = 0.6667 1.3333 fval = -8.2222 exitflag = 1 output = iterations: 3 algorithm: 'medium-scale: active-set' firstorderopt: [] cgiterations: [] message: 'Optimization terminated.' lambda = lower: [2x1 double] upper: [2x1 double] eqlin: [0x1 double] ineqlin: [3x1 double] exitflag = 1表示计算的退出条件是收敛于x。output是包含着优化信息的结构数组。lambda返回了x处包含拉格朗日乘子的参数。 5．有约束最小值优化 在有约束最优化问题中，通常要将该问题转换为更简单的子问题，对这些子问题可以求解并作为迭代过程的基础。早期的方法通常是通过构造惩罚函数等，将有约束的最优化问题转换为无约束最优化问题进行求解。现在，这些方法已经被更有效的基于K-T方程解的方法所取代。K-T方程是有约束最优化问题求解的必要条件。 MATLAB优化工具箱提供了fmincon函数用来计算有约束的最小值优化。 【例11-6】 求函数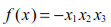 的最小值，搜索的起始值为x = [10;10;10]，同时目标函数中的变量要服从以下约束条件： 首先要写一个以x为变量的目标函数myfun3.m，该目标函数要返回一个标量。 myfun3.m function f = myfun3(x) f = -x(1) * x(2) * x(3); 其次，改写约束条件为小于或者等于一个常数的形式： 接下来，因为两个约束都是线性的，所以可以将其用矩阵来表示成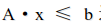 这种形式，其中： 然后调用fmincon函数进行优化： >> x0 = [10; 10; 10]; % 求解的起始点 >> A=[-1 -2 -2;1 2 2]; >> b=[0;72]; >> [x,fval] = fmincon(@myfun3,x0,A,b) x = 24.0000 12.0000 12.0000 fval = -3.4560e+003 最后可以对约束条件进行验证： >> A*x-b ans = -72 0
| 
/1 
|手机版|免责声明|本站介绍|工控课堂
( 沪ICP备20008691号-1 )
发表于 2019-2-2 21:36:01
提升卡
置顶卡
照妖镜
发表于 2019-2-2 21:53:54