基本概念 在图像处理中,高斯滤波一般用高斯模板。除此之外,还有递归高斯滤波、FFT法、重复卷积法等。 1、直接卷积法 2、重复卷积法 3、FFT实现法 原理很简单out = IFFT2(FFT(in)*FFT(h)),其中in是输入图像,h为卷积核,out是平滑后图像。 4、递归实现法 文献《Recursive implementation of the Gaussian filter》提出该方法,其产生一个IIR滤波器,比上面三种方法都快,其运行时间与σ无关。推导过程大致是,将高斯公式g(t)的傅里叶变换G(w)进行泰勒公式展开,阶数到6取近似,将其拉普拉斯变换G(s),在变换到z域时,用前后差分技术代替双线性法。最终结论如下。 q的选择如下 以上可以认为串行方式,还有并行方式,详细见文献《Recursively implementing the Gaussian and its derivatives》,在ITK中, itkRecursiveGaussianImageFilter实现了该算法。 示例演示 对图像进行高斯滤波而言,假设滤波器半径为r,我们常用的高斯模板则对于图像每个像素的算法复杂度是O(r^2)。高斯滤波器的kernel是可分离的(separable),也就是说,可以将2D的高斯kernel分解为两个1D的kernel,先沿x方向对图像进行1D高斯kernel的卷积,然后沿y方向对图像进行1D的高斯kernel卷积,最后的结果和使用一个2D高斯kernel对图像卷积效果是一样的。这样一来,针对每个像素,滤波器的算法复杂度降为O(r)。下面实现递归高斯滤波法,即上面第四种方法。完整工程代码。 /********************************************************************** Copyright (c) Mr.Bin. All rights reserved. For more information visit: http://blog.csdn.net/webzhuce **********************************************************************/ #include <opencv2/opencv.hpp> using namespace cv; typedef struct { int N; float sigma; double B; double b[4]; } GaussCoefs; /* * Calculate the coefficients for the recursive filter algorithm * Fast Computation of gaussian blurring. */ void ComputeGaussCoefs(GaussCoefs *c, float sigma) { /* * Papers: "Recursive Implementation of the gaussian filter.", * Ian T. Young , Lucas J. Van Vliet, Signal Processing 44, Elsevier 1995. * formula: 11b computation of q * 8c computation of b0..b1 * 10 alpha is normalization constant B */ float q = 0, q2 = 0, q3 = 0; if (sigma >= 2.5) { q = 0.98711 * sigma - 0.96330; } else if ((sigma >= 0.5) && (sigma < 2.5)) { q = 3.97156 - 4.14554 * (float)sqrt((double)1 - 0.26891 * sigma); } else { q = 0.1147705018520355224609375; } q2 = q * q; q3 = q * q2; c->b[0] = (1.57825 + (2.44413*q) + (1.4281 *q2) + (0.422205*q3)); c->b[1] = ((2.44413*q) + (2.85619*q2) + (1.26661 *q3)); c->b[2] = (-((1.4281*q2) + (1.26661 *q3))); c->b[3] = ((0.422205*q3)); c->B = 1.0 - ((c->b[1] + c->b[2] + c->b[3]) / c->b[0]); c->sigma = sigma; c->N = 3; } void RecursiveGausssmooth(float *in, float *out, int size, int rowstride, GaussCoefs *c) { /* * Papers: "Recursive Implementation of the gaussian filter.", * Ian T. Young , Lucas J. Van Vliet, Signal Processing 44, Elsevier 1995. * formula: 9a forward filter * 9b backward filter * fig7 algorithm */ int i, n, bufsize; float *w1, *w2; /* forward pass */ bufsize = size + 3; size -= 1; w1 = new float[bufsize]; w2 = new float[bufsize]; w1[0] = in[0]; w1[1] = in[0]; w1[2] = in[0]; for (i = 0, n = 3; i <= size; i++, n++) { w1[n] = (float)(c->B*in[i*rowstride] + ((c->b[1] * w1[n - 1] + c->b[2] * w1[n - 2] + c->b[3] * w1[n - 3]) / c->b[0])); } /* backward pass */ w2[size + 1] = w1[size + 3]; w2[size + 2] = w1[size + 3]; w2[size + 3] = w1[size + 3]; for (i = size, n = i; i >= 0; i--, n--) { w2[n] = out[i * rowstride] = (float)(c->B*w1[n] + ((c->b[1] * w2[n + 1] + c->b[2] * w2[n + 2] + c->b[3] * w2[n + 3]) / c->b[0])); } delete[] w1; delete[] w2; } /* @function: 2D gauss filter */ void RecursiveGausssmooth2D(const Mat &src, Mat &dst, float sigma = 1.0f) { GaussCoefs c; ComputeGaussCoefs(&c, sigma); const int height = src.rows; const int width = src.cols; if (src.channels() == 1) { Mat srccopy; src.convertTo(srccopy, CV_32FC1); Mat dstcopy; src.convertTo(dstcopy, CV_32FC1); float* srcdata = srccopy.ptr<float>(0); float* dstdata = dstcopy.ptr<float>(0); for (int y = 0; y < height; y++) { RecursiveGausssmooth(srcdata + y * width, dstdata + y * width, width, 1, &c); } for (int x = 0; x < width; x++) { RecursiveGausssmooth(dstdata + x, dstdata + x, height, width, &c); } dstcopy.convertTo(dst, src.type()); } else if (src.channels() == 3) { Mat srccopy; src.convertTo(srccopy, CV_32FC3); Mat dstcopy; src.convertTo(dstcopy, CV_32FC3); for (int y = 0; y < height; y++) { float* srcrowdata = srccopy.ptr<float>(y); float* dstrowdata = dstcopy.ptr<float>(y); RecursiveGausssmooth(srcrowdata, dstrowdata, width, 3, &c); RecursiveGausssmooth(srcrowdata + 1, dstrowdata + 1, width, 3, &c); RecursiveGausssmooth(srcrowdata + 2, dstrowdata + 2, width, 3, &c); } float* srcdata = srccopy.ptr<float>(0); float* dstdata = dstcopy.ptr<float>(0); for (int x = 0; x < width; x++) { RecursiveGausssmooth(dstdata + x * 3, dstdata + x * 3, height, width * 3, &c); RecursiveGausssmooth(dstdata + x * 3 + 1, dstdata + x * 3 + 1, height, width * 3, &c); RecursiveGausssmooth(dstdata + x * 3 + 2, dstdata + x * 3 + 2, height, width * 3, &c); } dstcopy.convertTo(dst, src.type()); } else return; } int main(int argc, char *argv[]) { Mat src = imread("../RecursiveGaussian/lena.bmp", 1); imshow("original", src); Mat dst; RecursiveGausssmooth2D(src, dst); imshow(" RecursiveGaussSmooth", dst); Mat dstImage; GaussianBlur(src, dstImage, Size(5, 5), 2, 2); imshow("GaussSmooth", dstImage); waitKey(0); return EXIT_SUCCESS; } 运行结果 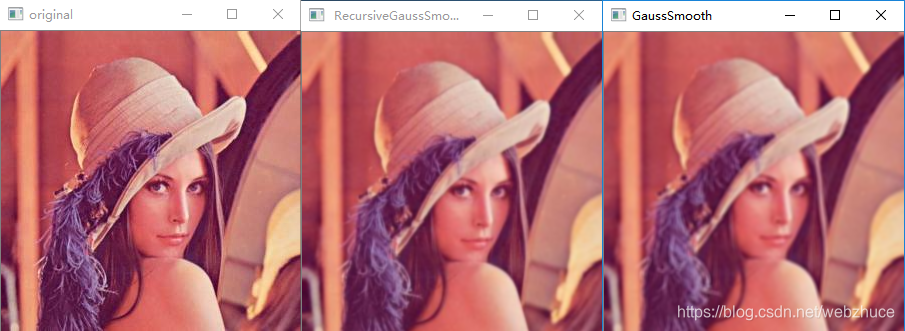 ———————————————— 版权声明:本文为CSDN博主「阿兵-AI医疗」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/webzhuce/article/details/100640543 |
 /1
/1 
 |手机版|免责声明|本站介绍|工控课堂
( 沪ICP备20008691号-1 )
|手机版|免责声明|本站介绍|工控课堂
( 沪ICP备20008691号-1 )
GMT+8, 2025-12-23 06:40 , Processed in 0.057604 second(s), 23 queries .
Powered by Discuz! X3.5
© 2001-2025 Discuz! Team.